Materi KPK dan FPB disertai Contoh Soal
KPK dan FPB
merupakan salah satu materi matematika yang cukup mudah untuk
dipelajari, karena materi FPB dan KPK merupakan implementasi dari
pemfaktoran yang artinya sama juga dengan penjulahan, pengurangan,
perkalian dan pembagian, itu sih menurut admin :) Untuk mencari FPB dan
KPK yang perlu kalian ketahui sebelumnya yaitu mengenai bilangan prima
dan faktorisasinya.
Intinya untuk mencari KPK adalah dengan memilih kelipatan terkecil dari 2 bilangan yang ditanyakan, sedangkan untuk mencari FPB yaitu dengan memilih faktor terbesar dari 2 bilangan yang ditanyakan. masih bingung dengan KPK dan FPB ? untuk lebih jelasnya silahkan lihat beberapa contoh soal KPK dan FPB dibawah.
Sebelum menginjak ke contoh soal penyelesaian FPB dan KPK mari kita mengingat kembali mengenai bilangan prima dan faktorisasi prima.
Contoh faktor prima dari 12 dan 18
dari gambar pohon faktor disamping kita dapat mengetahui :
fator prima dari 12
2 x 2 x 3
faktor prima dari 18
2 x 3 x3
KPK ialah nilai terkecil dari suatu kelipatan persekutuan 2 bilangan ataupun lebih bilangan.
Contoh soal : Carilah KPK dari 4 dan 8
Kelipatan 4 adalah = {4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, ....}
Kelipatan 8 adalah = {8, 16, 24. 32. 40, 48, 56, ...}
Jadi didapat kelipatan persekutuan dari 4 dan 8 adalah 8, 16, 24, 32, ... ( kelipatan yang bernilai sama dari 4 dan 8)
Nilai yang terkecil dari 2 kelipatan persekutuannya adalah 8, sehingga KPKdari 4 dan 8 adalah 8
-apabila ada yang sama ambilah yang terbesar, apabila keduanya sama ambil dari salah satunya
Contoh soal :
Carilah KPK dari 8, 12 dan 30
Buat pohon faktor KPK nya
Faktor Prima= 2x2x2 = 23 2x2x3 = 22 x 3 2 x 3 x 5
dari ketiga faktor 8, 12 dan 30 kita hanya menemukan 3 bilangan yaitu 2, 3 dan 5
faktor 2 yang terbesar àdalah 23
faktor 3 nilainyà sama untuk 12 dan 30 makà ambil salah satunyà yaitu 3
faktor 5 ada 1 àmbil nilai 5
sehingga didapat KPK dari 8, 12 dan 30 adalah 23 x 3 x 5 = 120
Contoh soal cerita materi KPK :
Jadi FPB adalah nilai paling besar dari faktor-faktor persekutuan dari 2 bilangan atau lebih itu.
Contoh :
Carilah FPB dari 4, 8 dan 12
Faktor dari 4 adalah = {1, 2, 4}
Faktor dari 8 adalah = {1, 2, 4, 8}
Faktor 12 adalah= {1, 2, 3, 4, 6, 12}
Jadi faktor persekutuan dari ketiga bilangan tersebut adalah 1, 2, 4
Nilai yang terbesarnya adalah 4, sehingga FPBnya adalah 4
Contoh : cari FPB dari 4, 8 dan 12
buat pohon faktornya
Faktor Prima= 2x2 = 22 2x2x2 = 23 2x 2 x 3 =22 x 3
faktor dari bilangan 4, 8 dan 12 yang sama adalah 2, dan yang terkecil adalah 22 = 4
Jadi FPB dari 4, 8 dan 12 adalah 4
Contoh soal cerita materi FPB :
Bu Aminah mempunyai 20 kelengkeng dan 30 anggur, kelengkeng dan anggur akan di masukkan kedalam plastik dengan jumlah yang sama besar.
a. Berapa plastik yang diperlukan untuk membungkus buah tersebut?
b. Berapa banyak kelengkeng dan anggur pada masing-masing plastik?
Jawab:
Faktorisasi prima dari 20 = 22 x 5
Faktorisasi prima dari 30 = 2 x 3 x 5
FPB dari 20 dan 30 = 2 x 5 = 10 ( kenapa yang dikalikan 2 dan 5, jika belum pahan baca lagi keatas)
a. Jumlah plastik yang diperlukan adalah 10 plastik
b. Jumlah kelengkeng dalam setiap plastik = 20/10 = 2 jeruk
Jujmlah anggur dalam setiap plastik = 30/10 = 3 salak
Demikian materi matematika FPB dan KPK yang bisa admin uraikan apabila kurang paham silahkan bertanya dalam kolom komentar atau like fanpage di facebook.com/MatematikaAcademy
Pengertian FPB dan KPK
Apasih kepanjangan dari kpk ? ingat lho kpk dalam matematika bukan kepanjangan dari komisi pemberantas korupsi, KPK dalam matematika biasa disebut dengan Kelipatan Persekutuan terKecil, sedang kepanjangan dari FPB adalah Faktor Persekutuan terBesar, udah jelaskan dengan pengertiannnya ?Intinya untuk mencari KPK adalah dengan memilih kelipatan terkecil dari 2 bilangan yang ditanyakan, sedangkan untuk mencari FPB yaitu dengan memilih faktor terbesar dari 2 bilangan yang ditanyakan. masih bingung dengan KPK dan FPB ? untuk lebih jelasnya silahkan lihat beberapa contoh soal KPK dan FPB dibawah.
Sebelum menginjak ke contoh soal penyelesaian FPB dan KPK mari kita mengingat kembali mengenai bilangan prima dan faktorisasi prima.
- Bilangan prima
- Faktorisasi prima
Contoh faktor prima dari 12 dan 18
dari gambar pohon faktor disamping kita dapat mengetahui :
fator prima dari 12
2 x 2 x 3
faktor prima dari 18
2 x 3 x3
KPK ( kelipatan persekutuan terkecil )
a. Cara mencari KPK dengan Kelipatan Persekutuan
Apa sih kelipatan persekutuan itu ? kelipatan persekutuan merupakan kelipatan yang sama dari 2 bilangan atau lebih .KPK ialah nilai terkecil dari suatu kelipatan persekutuan 2 bilangan ataupun lebih bilangan.
Contoh soal : Carilah KPK dari 4 dan 8
Kelipatan 4 adalah = {4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, ....}
Kelipatan 8 adalah = {8, 16, 24. 32. 40, 48, 56, ...}
Jadi didapat kelipatan persekutuan dari 4 dan 8 adalah 8, 16, 24, 32, ... ( kelipatan yang bernilai sama dari 4 dan 8)
Nilai yang terkecil dari 2 kelipatan persekutuannya adalah 8, sehingga KPKdari 4 dan 8 adalah 8
b. Cara mencari KPK dengan Faktorisasi Prima
- semua dari bilangan faktor dikalikan-apabila ada yang sama ambilah yang terbesar, apabila keduanya sama ambil dari salah satunya
Contoh soal :
Carilah KPK dari 8, 12 dan 30
Buat pohon faktor KPK nya
Faktor Prima= 2x2x2 = 23 2x2x3 = 22 x 3 2 x 3 x 5
dari ketiga faktor 8, 12 dan 30 kita hanya menemukan 3 bilangan yaitu 2, 3 dan 5
faktor 2 yang terbesar àdalah 23
faktor 3 nilainyà sama untuk 12 dan 30 makà ambil salah satunyà yaitu 3
faktor 5 ada 1 àmbil nilai 5
sehingga didapat KPK dari 8, 12 dan 30 adalah 23 x 3 x 5 = 120
Contoh soal cerita materi KPK :
FPB (Faktor Persekutuan terBesar)
a. Cara Mencari FPB dengan Faktor Persekutuan
Yang dimaksud dengan faktor persekutuan adalah faktor yang sama dari 2 bilangan ataupun lebih.Jadi FPB adalah nilai paling besar dari faktor-faktor persekutuan dari 2 bilangan atau lebih itu.
Contoh :
Carilah FPB dari 4, 8 dan 12
Faktor dari 4 adalah = {1, 2, 4}
Faktor dari 8 adalah = {1, 2, 4, 8}
Faktor 12 adalah= {1, 2, 3, 4, 6, 12}
Jadi faktor persekutuan dari ketiga bilangan tersebut adalah 1, 2, 4
Nilai yang terbesarnya adalah 4, sehingga FPBnya adalah 4
b. Cara Mencari FPB dengan Faktorisasi Prima
- ambilah bilangan faktor yang sama dan ambil yang terkecil dari 2 atau lebih bilangan yang didapat dari pemfaktoran tersebut.Contoh : cari FPB dari 4, 8 dan 12
buat pohon faktornya
Faktor Prima= 2x2 = 22 2x2x2 = 23 2x 2 x 3 =22 x 3
faktor dari bilangan 4, 8 dan 12 yang sama adalah 2, dan yang terkecil adalah 22 = 4
Jadi FPB dari 4, 8 dan 12 adalah 4
Contoh soal cerita materi FPB :
Bu Aminah mempunyai 20 kelengkeng dan 30 anggur, kelengkeng dan anggur akan di masukkan kedalam plastik dengan jumlah yang sama besar.
a. Berapa plastik yang diperlukan untuk membungkus buah tersebut?
b. Berapa banyak kelengkeng dan anggur pada masing-masing plastik?
Jawab:
Faktorisasi prima dari 20 = 22 x 5
Faktorisasi prima dari 30 = 2 x 3 x 5
FPB dari 20 dan 30 = 2 x 5 = 10 ( kenapa yang dikalikan 2 dan 5, jika belum pahan baca lagi keatas)
a. Jumlah plastik yang diperlukan adalah 10 plastik
b. Jumlah kelengkeng dalam setiap plastik = 20/10 = 2 jeruk
Jujmlah anggur dalam setiap plastik = 30/10 = 3 salak
Demikian materi matematika FPB dan KPK yang bisa admin uraikan apabila kurang paham silahkan bertanya dalam kolom komentar atau like fanpage di facebook.com/MatematikaAcademy
BILANGAN PECAHAN
Pecahan ! ya kali ini admin ingin menuliskan tentang pecahan, mulai dari
bilangan pecahan, pecahan campuran, pengertian pecahan dan lain
sebagainya. Meski tidak jelas materi matematika kelas berapa karena
admin agak lupa, tapi admin berharap paling tidak dapat membantu
adek-adek yang sedang ingin belajar bilangan pecahan.
Pengertian Pecahan
Ada yang tau pengertian pecahan ? yang belum tau yuk simak baik-baik apasih pecahan itu ?
Bilangan pecahan merupakan sebuah bilangan yang terdiri dari pembilang dan juga penyebut. perhatikan gambar.
ya, yang namanya pembilang selalu berada diatas dan penyebut selalu
dibawah, dalam melakukan operasi pecahan lebih mudahnya dengan
menyederhanakan pembilang maupun penyebutnya. Misalnya 50/100 tampak
besarkan bilangannya padahal jika kita sederhanakan nilai 50/100 sama
dengan nilai 1/2. lebih mudah mana operasi dengan bilangan besar atau
kecil ? tentunya lebih mudah yang kecil kan ?. :D
Untuk mempelajari cara menyederhanakan penyebut kalian bisa menuju ke sini, gimana dengan uraian diatas kalian sudah dapat memahami apa itu pecahankan ? oke mari kita lanjut ke jenis-jenis pecahan.
Jenis-jenis pecahan
Bilangan pecahan terbagi menjadi 3 yaitu : pecahan biasa, pecahan desimal dan pecahan campuran.
Bilangan pecahan biasa
Jenis pecahan yang pertama yaitu pecahan biasa yang sudah biasa kita temukan seperti 1/2, 1/3, 1/4, 1/5 cara bacanya :
1/2 => setengah
1/3 => sepertiga
1/4 => seperempat
1/5 => seperlima
2/3 => dua per tiga dan seterusnya.
Bilangan pecahan desimal
Pecahan desimal biasanya dituliskan dalam bentu nol koma. misal 0,1
siswa : pak tadi katanya pecahan itu terdiri dari pembilang dan penyebut ? la itu ?
guru : pertanyaan bagus !!
0,1 jika dituliskan dalam bentuk pembilang penyebut akan menjadi 1/10
kenapa persepuluh, karena hanya ada satu angka dibelakang koma, jika
pecahan desimalnya 0,01 maka pecahan biasanya akan menjadi 1/100.
semakin banyak angka di belakang koma maka semakin besar pula
penyebutnya. contoh lainnya:
0,25 => nol koma dua lima
0,5 => nol koma lima
dst...
Bilangan pecahan campuran
Bilangan pecahan campuran yaitu bilangan pecahan biasa yang dicampur
dengan bilangan bulat, makanya disebut dengan bilangan pecahan campuran.
1 1/2 => satu, setengah
2 2/3 => dua, dua per tiga
34 78/93 => tiga puluh empat, tujuh delapan per sembilan tiga
Demikian uraian dari admin yang bisa diberikan di blog ini juga sudah banyak membahas tentang pecahan kok seperti di cara menghitung perkalian pecahan campuran dan banyak lagi, karena sudah cukup larut malem admin sudahi dulu postingan kali ini. selamat belajar PECAHAN.
Materi Bilangan Berpangkat
Berikut sedikit penjelasan mengenai materi matematika " Bilangan Berpangkat " yang admin rangkum dari BSE matematika sma kelas x kurikulum 2013,
Dengan mempelajari materi ini kalian diharapkan dapat : mengalikan dua bilangan berpangkat yang bilangan pokoknya sama, memangkatkan bilangan berpangkat, memangkatkan dari pembagian dua bilangan, mengubah pangkat pecahan ke bentuk akar pangkat, membagi dua bilangan berpangkat yang bilangan pokoknya sama, memangkatkan dari perkalian dua bilangan, , dan mengubah pangkat negatif ke pangkat positif.
Contoh :
a. 23 x 22 = 23+2 = 25
b. 10-1 x 105 = 10-1+5 = 104
c. 5 x 55 = 51+5 = 56
Contoh :
a. 23 : 22 = 23-2 = 21 = 2
b. 10-1 : 105 = 10-1-5 = 10-6
c. 5 : 55 = 51-5 = 5-4
contoh :
a. (34)2 = 34x2 = 38
b. (6-2)3 = 6-2x3 = 6-6
Contoh :
a. (2 x 5)2 = 22 x 52 = 4 x 25 = 100
b. 24 x 54 = (2 x 5)4 = 104 = 10000
Contoh :
a. (2 : 5)2 = 22 : 52 = 4 : 25 = 1/4
b. 24 : 54 = (2 : 5)4
Demikian sedikit pemaparan mengenai materi bilangan berpangkat yang bisa admin berikan dan semoga bermanfaat buat kalian, terus semangat untuk belajar jangan pernah menyerah dan banyak-banyak berlatih soal-soal matematika agar kalian terbiasa.
Selamat belajar bilangan berpangkat
Dengan mempelajari materi ini kalian diharapkan dapat : mengalikan dua bilangan berpangkat yang bilangan pokoknya sama, memangkatkan bilangan berpangkat, memangkatkan dari pembagian dua bilangan, mengubah pangkat pecahan ke bentuk akar pangkat, membagi dua bilangan berpangkat yang bilangan pokoknya sama, memangkatkan dari perkalian dua bilangan, , dan mengubah pangkat negatif ke pangkat positif.
Pengertian Bilangan Berpangkat
Dalam memahami pengertian bilangan berpangkat dapat dijelaskan melalui rumus berikut :
an = a x a x a x a x a ... x a sebanyak n
Aturan dasar pengoperasian bilangan berpangkat
Berikut 8 rumus dalam materi bilangan berpangkat yang admin rasa kalian harus memahami konsepnya karena akan sangat berguna untuk penyelesaian soal-soal matematika yang berhubungan dengan pangkat. yuk simak baik-baik.- Perkalian bilangan berpangkat yang bilangan pokoknya sama
Contoh :
a. 23 x 22 = 23+2 = 25
b. 10-1 x 105 = 10-1+5 = 104
c. 5 x 55 = 51+5 = 56
- Pembagian bilangan berpangkat yang bilangan pokoknya sama besar
Contoh :
a. 23 : 22 = 23-2 = 21 = 2
b. 10-1 : 105 = 10-1-5 = 10-6
c. 5 : 55 = 51-5 = 5-4
- Pemangkatan bilangan berpangkat
contoh :
a. (34)2 = 34x2 = 38
b. (6-2)3 = 6-2x3 = 6-6
- Pemangkatan dari perkalian dua bilangan
Contoh :
a. (2 x 5)2 = 22 x 52 = 4 x 25 = 100
b. 24 x 54 = (2 x 5)4 = 104 = 10000
- Pemangkatan dari pembagian dua bilangan
Contoh :
a. (2 : 5)2 = 22 : 52 = 4 : 25 = 1/4
b. 24 : 54 = (2 : 5)4
- Bilangan berpangkat negatif
- Bilangan berpangkat pecahan
Demikian sedikit pemaparan mengenai materi bilangan berpangkat yang bisa admin berikan dan semoga bermanfaat buat kalian, terus semangat untuk belajar jangan pernah menyerah dan banyak-banyak berlatih soal-soal matematika agar kalian terbiasa.
Selamat belajar bilangan berpangkat
BSE Materi Matematika SMP Kelas 7 Kurikulum 2013 terbitan 2014
BSE matematika SMP / Mts kelas 7 kurikulum 2013
terbitan tahun 2014 akhirnya admin temukan juga di website resmi
kemendikbud, berikut daftar bab dan sub bab yang harus kalianpelajari
dibangku smp khususnya materi matematika :
Bab 1 Bilangan
1.1 membandingkan bilangan bulat
1.2 menjumlahkan dan mengurangkan bilangan bulat
1.3 mengalikan dan membagi bilangan bulat
1.4 kelipatan dan faktor bilangan bulat
1.5 membandingkan bilangan pecahan
1.6 menjumlahkan dan mengurangkan bilangan pecahan
1.7 mengalikan dan membagi bilangan bilangan pecahan
1.8 memahami bilangan rasional
1.9 memahami pola bilangan
Bab 2 Himpunan
2.1 memahami konsep himpunan dan diagram venn
2.2 memahami relasi himpunan
2.3 memahami operasi himpunan
Bab 3 Perbandingan
3.1 memahami perbandingan
3.2 menentukan perbandingan dua besaran dengan satuan yang berbeda
3.3 menyelesaikan masalah proporsi
3.4 menyelesaikan masalah skala
Bab 4 Garis dan sudut
4.1 memahami kedudukan garis dan sudut
4.2 memahami hubungan antar sudut
Didalam buku sekolah elektronik ini yang sering disebut dengan BSE juga terdapat latihan matematika per subabnya jadi jangan khawatir bagi kalian yang suka dengan tantangan soal-soal matematika karena anda tidak akan kekurangan soal
Download BSE matematika SMP/Mts kelas 7 kurikulum 2013 terbitan tahun 2014 disini
Demikian artikel sederhana sore ini silahkan kalian unduh materi matematika tersebut sebagai perlengkapan tambahan dalam menimba ilmu matematika di sekolah khususnya jemjang SMP / Mts kelas VII. semoga bermanfaat.
 | |
| Cover bse matematika kelas 7 |
1.1 membandingkan bilangan bulat
1.2 menjumlahkan dan mengurangkan bilangan bulat
1.3 mengalikan dan membagi bilangan bulat
1.4 kelipatan dan faktor bilangan bulat
1.5 membandingkan bilangan pecahan
1.6 menjumlahkan dan mengurangkan bilangan pecahan
1.7 mengalikan dan membagi bilangan bilangan pecahan
1.8 memahami bilangan rasional
1.9 memahami pola bilangan
Bab 2 Himpunan
2.1 memahami konsep himpunan dan diagram venn
2.2 memahami relasi himpunan
2.3 memahami operasi himpunan
Bab 3 Perbandingan
3.1 memahami perbandingan
3.2 menentukan perbandingan dua besaran dengan satuan yang berbeda
3.3 menyelesaikan masalah proporsi
3.4 menyelesaikan masalah skala
Bab 4 Garis dan sudut
4.1 memahami kedudukan garis dan sudut
4.2 memahami hubungan antar sudut
Didalam buku sekolah elektronik ini yang sering disebut dengan BSE juga terdapat latihan matematika per subabnya jadi jangan khawatir bagi kalian yang suka dengan tantangan soal-soal matematika karena anda tidak akan kekurangan soal
Download BSE matematika SMP/Mts kelas 7 kurikulum 2013 terbitan tahun 2014 disini
Demikian artikel sederhana sore ini silahkan kalian unduh materi matematika tersebut sebagai perlengkapan tambahan dalam menimba ilmu matematika di sekolah khususnya jemjang SMP / Mts kelas VII. semoga bermanfaat.
Barisan dan Geret Geometri Materi Matematika SMP
Untuk mempelajari materi materi matematika barisan geometri dan deret geometri ada baiknya kalian memahami lebih dulu materi Barisan dan deret aritmatika silahkan menuju link tersebut. Barisan bilangan seperti apasih yang disebut dengan barisan geometri ?
Suatu barisan U1, U2, U3,U4, ... Un disebut sebagai barisan geometri jika perbandingan dua suku yang berurutan selalu tetap. Perbandingan antara dua suku yang berurutan itu disebut pembanding atau rasio, biasanya dilambangkan dengan " r "
jadi r = U2/U1 = U3/U2 = U4/U3 = ... = Un
apabila suku pertama dinyatakan dengan a maka bentuk barisan geometrinya mejadi :
a, ar, ar2, ar3, ... arn-1
Nah gimana udah paham dengan apa itu barisan geometri, kalo udah paham mari lanjut ke pembahasan deret geometri.
Pada deret geometri U1 + U2 + U3 + U4, ... Un
jika :
Un+1 > Un maka deretnya disebut deret geometri naik, sebaliknya jika
Un+1 < Un maka deretnya disebut deret geometri turun.
Contoh Soal Deret geometri :
Diketahui deret 2 + 6 + 18 + 54 + 162 + ...
U2/U1 = 6/2 = 3
U3/U2 = 18/6 = 3
U4/U3 = 54/18 = 3
Karena rasionya tetap yaitu 3 maka deret diatas disebut dengan deret geometri, dan karena Un+1 > Un maka deret tersebut termasuk deret geometri naik.
Diketahui deret geometri 3 + 6 + 12 + 24 + ... tentukan suku ke-13 dari deret geometri tersebut.
penyelesaian :
r = u2/u1 = 6/3 = 2
rumus suku ke-n (Un) = arn - 1
Suku ke-13 U = 3 x 213-1 = 3 x 212 = 3x 4.096 = 12.288
Jumlah n suku pertama pada deret geometri
Untuk mengetahui jumlah n suku ( Sn ) dari deret geometri dapat ditentukan dengan rumus sebagai berikut :
Hubungan Un dan Sn adalah Un = Sn - Sn-1
Contoh Soal :
Tentukan Jumlah 6 suku pertama dari deret geometri 3 + 6 + 12 + 24 + ...
Penyelesaian :
a = 3
n = 6
r = 6/3 = 2, r >1
Lihat rumus Sn diatas maka ;
S6 = 3 ( 26- 1 ) / 2 -1 = 3 x 63 / 1 = 3 x 63 = 189
Nah mudahkan untuk menentukan jumlah n suku dari deret geometri yang menurut saya beda-beda tipislah sama deret aritmatika, nah yang perlu diingat adalah dalam penerapan rumus deret aritmatika dengan rumus deret geometri jangan sampai tertukar karena biasanya hal tersebut sering terjadi.
Demikian pos kali ini mengenai deret geometri semoga bermanfaat dan
S E L A M A T _ B E L A J A R
 |
| ilustrasi barisan dan deret geometri |
Suatu barisan U1, U2, U3,U4, ... Un disebut sebagai barisan geometri jika perbandingan dua suku yang berurutan selalu tetap. Perbandingan antara dua suku yang berurutan itu disebut pembanding atau rasio, biasanya dilambangkan dengan " r "
jadi r = U2/U1 = U3/U2 = U4/U3 = ... = Un
apabila suku pertama dinyatakan dengan a maka bentuk barisan geometrinya mejadi :
a, ar, ar2, ar3, ... arn-1
Nah gimana udah paham dengan apa itu barisan geometri, kalo udah paham mari lanjut ke pembahasan deret geometri.
Pada deret geometri U1 + U2 + U3 + U4, ... Un
jika :
Un+1 > Un maka deretnya disebut deret geometri naik, sebaliknya jika
Un+1 < Un maka deretnya disebut deret geometri turun.
Contoh Soal Deret geometri :
Diketahui deret 2 + 6 + 18 + 54 + 162 + ...
U2/U1 = 6/2 = 3
U3/U2 = 18/6 = 3
U4/U3 = 54/18 = 3
Karena rasionya tetap yaitu 3 maka deret diatas disebut dengan deret geometri, dan karena Un+1 > Un maka deret tersebut termasuk deret geometri naik.
Rumus Suku ke-n Deret Geometri
Jika suku pertama dinyatakan dengan a, banyaknya suku dinyatakan dengan
n, dan r menyatakan rasio maka suku ke-n dari deret geometri dapat
dirumuskan sebagai berikut :
Un = arn - 1
Contoh soal :Diketahui deret geometri 3 + 6 + 12 + 24 + ... tentukan suku ke-13 dari deret geometri tersebut.
penyelesaian :
r = u2/u1 = 6/3 = 2
rumus suku ke-n (Un) = arn - 1
Suku ke-13 U = 3 x 213-1 = 3 x 212 = 3x 4.096 = 12.288
Jumlah n suku pertama pada deret geometri
Untuk mengetahui jumlah n suku ( Sn ) dari deret geometri dapat ditentukan dengan rumus sebagai berikut :
Hubungan Un dan Sn adalah Un = Sn - Sn-1
Contoh Soal :
Tentukan Jumlah 6 suku pertama dari deret geometri 3 + 6 + 12 + 24 + ...
Penyelesaian :
a = 3
n = 6
r = 6/3 = 2, r >1
Lihat rumus Sn diatas maka ;
S6 = 3 ( 26- 1 ) / 2 -1 = 3 x 63 / 1 = 3 x 63 = 189
Nah mudahkan untuk menentukan jumlah n suku dari deret geometri yang menurut saya beda-beda tipislah sama deret aritmatika, nah yang perlu diingat adalah dalam penerapan rumus deret aritmatika dengan rumus deret geometri jangan sampai tertukar karena biasanya hal tersebut sering terjadi.
Demikian pos kali ini mengenai deret geometri semoga bermanfaat dan
S E L A M A T _ B E L A J A R
Materi Barisan dan Deret Aritmatika Lengkap dengan Rumus
Masih seputar materi aritmatika,
yang semangat ya kawan-kawan kita masih akan belajar mengenai barisan
aritmatika dan deret aritmatika. yuk baca dengan seksama.
jadi nilai selisih dari baris bilangan dapat kita tuliskan sperti berikut :
b = U2 - U1 = U4 - U3 = U6 - U5 ... = Un - Un-1
Jika suku pertama dalam barisan aritmatika dinyatakan dengan a, maka didapat bentuk umum dari barisan aritmatika yaitu :
a, a+b, a+2b, a+3b, a+4b,.... a+(n-1)b
a = suku pertama
b = beda
Jadi, Rumus suku ke-n barisan aritmatika adalah sebagai berikut
Un = a + ( n - 1 ) b
b = U2 - U1 = U4 - U3 =
karena barisan bilangan tersebut mempunyai beda yang tetap yaitu 3 maka barisan tersebut merupakan barisan aritmatika.
b) 2, 5, 7, 9, ...
U2 - U1 = 3
U3 - U2 = 2
karena beda dari barisan bilangan tersebut tidak konstan/ tidak tetap maka barisan bilangan tersebut bukan barisan aritmatika.
Demikian materi barisan aritmatika dan deret aritmatika yang bisa admin
berikan semo kalian dapat memahami rumus barisan aritmatika serta rumus
jumlah deret aritmatikanya.
selamat belajar !!!
Barisan Aritmatika
Sedikit banyak pastinya kalian sudah taukan apa itu barisan matematika kan ? bagi yang belum tau perlu diketahui bahwa barisan bilangan dinyatakan dalam bentuk U1, U2, U3,U4, ... Un baris bilangan seperti ini disebut dengan baris bilangan aritmatika, jika selisih dua suku berurutan selau tetap, dan selanjutnya selisih tersebut disebut dengan beda dan dilambangkan dengan huruf bjadi nilai selisih dari baris bilangan dapat kita tuliskan sperti berikut :
b = U2 - U1 = U4 - U3 = U6 - U5 ... = Un - Un-1
Jika suku pertama dalam barisan aritmatika dinyatakan dengan a, maka didapat bentuk umum dari barisan aritmatika yaitu :
a, a+b, a+2b, a+3b, a+4b,.... a+(n-1)b
a = suku pertama
b = beda
Jadi, Rumus suku ke-n barisan aritmatika adalah sebagai berikut
Un = a + ( n - 1 ) b
Contoh soal barisan aritmatika :
a) 1, 4, 7, 10, ...b = U2 - U1 = U4 - U3 =
karena barisan bilangan tersebut mempunyai beda yang tetap yaitu 3 maka barisan tersebut merupakan barisan aritmatika.
b) 2, 5, 7, 9, ...
U2 - U1 = 3
U3 - U2 = 2
karena beda dari barisan bilangan tersebut tidak konstan/ tidak tetap maka barisan bilangan tersebut bukan barisan aritmatika.
Deret Aritmatika
Deret aritmatika adalah jumlah semua suku-suku pada barisan aritmatika,
deret artitmatika juga biasa disebut dengan deret hitung. Deret
aritmatika yang mempunyai beda lebih dari nol atau positif, maka
deretnya disebut dengan deret aritmatika naik. Sedangkan deret
aritmatika yang mempunyai beda kurang dari nol atau negatif maka
deretnya disebut deret menurun.
Bentuk umum deret aritmatika :
a + ( a+b ) + ( a+2b ) + ( a +3b ) + ... + { a+(n-1)b}
Rumus suku ke-n deret aritmatika
Apabila a menyatakan suku pertama, n menyatakan banyak suku dan b merupakan beda suatu barisan aritmatka maka :
selamat belajar !!!
Segitiga Pascal Pada Materi Pola Bilangan
Materi bilangan terbanyak terdapat banyak sekali fakta menarik dalam segitiga Pascal.
Setiap baris segitiga Pascal memuat bilangan yang merupakan koefisien
dari bentuk ekspansi pangkat bilangan cacah dari binomial. Akan tetapi,
pada pembahasan ini admin akan dikhususkan untuk menemukan pola bilangan
dalam tiap diagonal segitiga Pascal tersebut. Perhatikan gambar
segitiga pascal berikut.
Untuk menemukan sebuah pola tersebut kita membutuhkan pola bilangan dalam tiap baris segitiga Pascal. Semua bilangan dalam tiap-tiap baris tersebut merupakan koefisien dari ekspansi pangkat binomial. perhatikan contoh :
Lihat pada gambar segitiga pascal diatas perhatikan pada i=4 Koefisien ekspansi pangkat 4 binomialnya adalah 1, 4, 6, 4, dan 1 yang merupakan bilangan-bilangan pada baris ke-4 pada segitiga Pascal. Menurut Teorema Binomial,
Dari uraian diatas secara umum dapat kita simpulkan bahwa barisan bilangan pada baris i = k dalam segitiga Pascal dapat dituliskan sebagai berikut :
Sebagai contohnya, bilangan ke-3 dan ke-2 dari baris ke-5 pada segitiga Pascal adalah,
Berdasarkan pola tersebut kita dapat menentukan sebuah rumus untuk menentukan bilangan ai,j,yaitu bilangan yang terdapat pada kolom ke-j dan baris ke-i dalam segitiga pascal.
misalnya kita akan menentukan pada baris ke-7 dan kolom ke-6 maka akan menjadi seperti berikut:
Dari rumus ai,j diatas, kita dapat menuliskan sebuah barisan bilangan pada diagonal ke-d seperti berikut.
Sehingga didapat suku ke-n dari baris bilangan pada diagonal ke-d adalah
Sebagai contohnya, diagonal ke-3 pada segitiga Pascal yang merupakan bilangan-bilangan segitiga yang berpola n(n + 1)/2. Pada barisan ini akan kita uji menggunakan rumus yang baru saja diketemukan. Dengan d = 3,
Demikian uraian mengenai segitiga pascal yang bisa admin share semoga dengan sedikit materi matematika tersebet sedikit banyak dapat bermanfaat pada kita semua. selamat memahami apa itu segitiga pascal segitiga pascal
Selamat belajar.
Untuk menemukan sebuah pola tersebut kita membutuhkan pola bilangan dalam tiap baris segitiga Pascal. Semua bilangan dalam tiap-tiap baris tersebut merupakan koefisien dari ekspansi pangkat binomial. perhatikan contoh :
Lihat pada gambar segitiga pascal diatas perhatikan pada i=4 Koefisien ekspansi pangkat 4 binomialnya adalah 1, 4, 6, 4, dan 1 yang merupakan bilangan-bilangan pada baris ke-4 pada segitiga Pascal. Menurut Teorema Binomial,
Dari uraian diatas secara umum dapat kita simpulkan bahwa barisan bilangan pada baris i = k dalam segitiga Pascal dapat dituliskan sebagai berikut :
Sebagai contohnya, bilangan ke-3 dan ke-2 dari baris ke-5 pada segitiga Pascal adalah,
Berdasarkan pola tersebut kita dapat menentukan sebuah rumus untuk menentukan bilangan ai,j,yaitu bilangan yang terdapat pada kolom ke-j dan baris ke-i dalam segitiga pascal.
misalnya kita akan menentukan pada baris ke-7 dan kolom ke-6 maka akan menjadi seperti berikut:
Dari rumus ai,j diatas, kita dapat menuliskan sebuah barisan bilangan pada diagonal ke-d seperti berikut.
Sehingga didapat suku ke-n dari baris bilangan pada diagonal ke-d adalah
Sebagai contohnya, diagonal ke-3 pada segitiga Pascal yang merupakan bilangan-bilangan segitiga yang berpola n(n + 1)/2. Pada barisan ini akan kita uji menggunakan rumus yang baru saja diketemukan. Dengan d = 3,
Demikian uraian mengenai segitiga pascal yang bisa admin share semoga dengan sedikit materi matematika tersebet sedikit banyak dapat bermanfaat pada kita semua. selamat memahami apa itu segitiga pascal segitiga pascal
Selamat belajar.
Pola Bilangan Matematika
Materi Pola bilangan
yang merupakan sub bab dari materi barisan aritmatika untuk SMP disini
kta akan membahas mengenai pola bilangan ganjil dan pola bilangan genap,
Apa itu pola bilangan ?
Pola ialah sebuah susunan yang mempunyai bentuk teratur, sedang bilangan itu sendiri ialah sesuatu yang digunakan untuk menunjukkan kuantitas ( banyak/sedikit ) dan ukuran ( ringan / berat / pendek / panjang / luas ). Bilangan ditunjukkan oleh suatu tanda atau lambang yang disebut angka teratur dari bentuk satu ke bentuk lainnya.
Dalam beberapa kasus kita temui seuah bilangan yang tersusun dari bilangan lain yang mempunyai pola tertentu, maka yg demikian disebut sebagai pola bilangan.
Contoh soal :
Tentukanlah jumlah 7 bilangan asli ganjil yang pertama !
jawab :
ketujuh bilangan tersebut adalah : 1, 3, 5, 7, 9, 11, 13. jadi n=7
jumlah ke-7 bilangan tersebut adalah 72=49
untuk membuktikan silahkan dihitung manual 1+3+5+7+9+11+13=...?
Contoh 2 pola bilangan
Berapakah banya bilangan asli ganjil yang jumlahnya 81 ?
jawab :
Kita telah mengetahui bahwa jumlah bilangan asli ganjil yaitu banyaknya bilangan asli ganjil dikuadratkan secara sederhana dapat kita tuliskan n2 dari pertanyaan diatas dapat kita simpulkan bahwa
n2=81, maka
n = √81
n = 9, jadi banyaknya bilangan ganjil adalah 9.
Perhatikan susunan heksagonal seperti pada gambar berikut :
Gambar diatas menunjukkan bahwa heksagonal yang terdiri sebanyak bilangan genap dapat disusun membentuk pola tertentu. sehingga gambar diatas bisa disebut sebagai pola bilangan genap.
Untuk lebih memahami perhatikan uraian penjumlahan bilangan asli genap berikut :
Penjumlahan dari 2 bilangan genap :
2 + 4 = 6, n=2 dapat ditulis 6 = 2 (2+1)
penjumlahan 3 bilangan genap :
2 + 4 + 6 = 12, n=3 dapat ditulis 12 = 3 ( 3+1)
penjulahan 4 bilangan genap :
2 + 4 + 6 + 8 = 20, n=4 dapat ditulis 20 = 4 (4+1)
dari pola di atas seharusnya anda sudah dapat menarik kesimpulan rumus jumlah pola bilangan genap, ya benar rumusnya adalah ns = n ( n + 1 )
Untuk mengaplikasikan rumus tersebut silahkan kalian kerjaan soal berikut :
Apa itu pola bilangan ?
Pola ialah sebuah susunan yang mempunyai bentuk teratur, sedang bilangan itu sendiri ialah sesuatu yang digunakan untuk menunjukkan kuantitas ( banyak/sedikit ) dan ukuran ( ringan / berat / pendek / panjang / luas ). Bilangan ditunjukkan oleh suatu tanda atau lambang yang disebut angka teratur dari bentuk satu ke bentuk lainnya.
Dalam beberapa kasus kita temui seuah bilangan yang tersusun dari bilangan lain yang mempunyai pola tertentu, maka yg demikian disebut sebagai pola bilangan.
Pola Bilangan Genap dan Bilangan Ganjil
Pola Bilangan Genap
Salah satu himpunan dari bilangan asli adalah bilangan ganjil. apa itu bilangan ganjil ? Bilangan ganjil adalah bilangan asli yang tak habis jika dibagi dengan 2 atau kelipatannya.Contoh soal :
Tentukanlah jumlah 7 bilangan asli ganjil yang pertama !
jawab :
ketujuh bilangan tersebut adalah : 1, 3, 5, 7, 9, 11, 13. jadi n=7
jumlah ke-7 bilangan tersebut adalah 72=49
untuk membuktikan silahkan dihitung manual 1+3+5+7+9+11+13=...?
Contoh 2 pola bilangan
Berapakah banya bilangan asli ganjil yang jumlahnya 81 ?
jawab :
Kita telah mengetahui bahwa jumlah bilangan asli ganjil yaitu banyaknya bilangan asli ganjil dikuadratkan secara sederhana dapat kita tuliskan n2 dari pertanyaan diatas dapat kita simpulkan bahwa
n2=81, maka
n = √81
n = 9, jadi banyaknya bilangan ganjil adalah 9.
Pola Bilangan Genap
Selain bilangan ganjil, bilangan genap juga termasuk anggota dari bilangan asli yaitu {2, 4, 6, 8, ...}Perhatikan susunan heksagonal seperti pada gambar berikut :
Gambar diatas menunjukkan bahwa heksagonal yang terdiri sebanyak bilangan genap dapat disusun membentuk pola tertentu. sehingga gambar diatas bisa disebut sebagai pola bilangan genap.
Untuk lebih memahami perhatikan uraian penjumlahan bilangan asli genap berikut :
Penjumlahan dari 2 bilangan genap :
2 + 4 = 6, n=2 dapat ditulis 6 = 2 (2+1)
penjumlahan 3 bilangan genap :
2 + 4 + 6 = 12, n=3 dapat ditulis 12 = 3 ( 3+1)
penjulahan 4 bilangan genap :
2 + 4 + 6 + 8 = 20, n=4 dapat ditulis 20 = 4 (4+1)
dari pola di atas seharusnya anda sudah dapat menarik kesimpulan rumus jumlah pola bilangan genap, ya benar rumusnya adalah ns = n ( n + 1 )
Untuk mengaplikasikan rumus tersebut silahkan kalian kerjaan soal berikut :
- Tentukan jumlah 10 bilangan asli pertama !
- Tentukan jumlah 8 bilangan asli pertama !
Materi Skala dan Perbandingan
Berbicara soal skala pasti yang teringat skala peta, bagaimana sih pembacaan skala pada peta ? perhatikan uraian berikut :
Sebuah desain rumah digambarkan dengan skala 1 : 50, arti dari skala 1 : 50 yaitu setiap jarak satu centimeter pada gambar mewakili 50 centimeter jarak sesungguhnya. Jika panjang rumah pada gambar desain ditunjukkan dengan jarak 10 cm maka panjang rumah yang sesungguhnya adalah 10 x 50 cm = 500 cm.
Dari uraian tadi dapat ikita tarik sebuah kesimpulan mengenai pengertian dari skala.
Skala adalah perbandngan antara jarak pada gambar dengan jarak sesungguhnya. Skala biasanya digunakan pada denah lokasi, peta, dan rancangan benda.
Contoh penulisan skala :
1 : 20.000, 1 : 15.000, dan 1 : 1.750.000
Contoh soal skala :
Sebuah peta dengan skala 1 : 25.000, berapakah jarak sesungguhnya jika pada peta ditunjukkan dengan jarak 4 cm.
jawab :
jarak pada peta 4 cm
jarak sebenarnya adalah 4 x 25.000 cm = 100.000 cm
contoh perbandingan senilai:
maka berlaku a1/a2 = b1/b2
contoh perbandingan berbalik nilai :
a1/a2 = b2/b1
Demikian materi skala dan perbandingan baik yang senilai maupun berbalik nilai yang bisa disampaikan untuk soal-soal mengenai skala dan perbandingan silahkan ditunggu untuk posting selanjutnya.
selamat belajar dan semoga bermanfaat.
Sebuah desain rumah digambarkan dengan skala 1 : 50, arti dari skala 1 : 50 yaitu setiap jarak satu centimeter pada gambar mewakili 50 centimeter jarak sesungguhnya. Jika panjang rumah pada gambar desain ditunjukkan dengan jarak 10 cm maka panjang rumah yang sesungguhnya adalah 10 x 50 cm = 500 cm.
Dari uraian tadi dapat ikita tarik sebuah kesimpulan mengenai pengertian dari skala.
Skala adalah perbandngan antara jarak pada gambar dengan jarak sesungguhnya. Skala biasanya digunakan pada denah lokasi, peta, dan rancangan benda.
Contoh penulisan skala :
1 : 20.000, 1 : 15.000, dan 1 : 1.750.000
Rumus Skala
Contoh soal skala :
Sebuah peta dengan skala 1 : 25.000, berapakah jarak sesungguhnya jika pada peta ditunjukkan dengan jarak 4 cm.
jawab :
jarak pada peta 4 cm
jarak sebenarnya adalah 4 x 25.000 cm = 100.000 cm
Bentuk-bentuk Perbandingan
Perbaningan Senilai
Apa sih maksud dari perbandingan senilai, perbandingan senilai yaitu perbandingan yang mempunyai sifat besaran jika yang satu bertambah, besaran lain juga bertambah pula.contoh perbandingan senilai:
- Banyak pensil yang dibeli dengan besar uang untuk membayar
- Jarak dengan kecepatannya
maka berlaku a1/a2 = b1/b2
Perbandingan berbalik nilai
Sebuah perbandingan termasuk dalam perbandingan berbalik nilai jika perbandingan mempunyai sifat bila besaran satu bertambah besar maka besaran lain justru bertambah kecil.contoh perbandingan berbalik nilai :
- Banyak pekerja dengan waktu yang ditetapkan untuk penyelesaian
- waktu perjalanan dengan kecepatan.
a1/a2 = b2/b1
Demikian materi skala dan perbandingan baik yang senilai maupun berbalik nilai yang bisa disampaikan untuk soal-soal mengenai skala dan perbandingan silahkan ditunggu untuk posting selanjutnya.
selamat belajar dan semoga bermanfaat.
Materi Bilangan Pecahan biasa, desimal, persen
Bentuk umum dari pecahan yaitu a/b dibaca a per b dengan a dan b merupakan bilangan bulat serta b tidak sama dengan nol ( 0 ).
pecahan a/b
a disebut dengan pembilang
b disebut dengan penyebut.
Jika pembilang dan penyebut suatu pecahan dikali ataupun dibagi dengan bilangan yang sama besar maka akan didapat pecahan yang senilai.
misal :
1/2 dikali dengan 2/2 maka hasilnya 2/4, nilai 1/2 = 2/4. meski bilangan pembilang dan penyebutnya berbeda akan tetapi nilainya tetap sama. Ingat invers dari perkalian ? ya benar berapapun bilangannya jika dikalikan dengan satu maka hasilnya adalah bilangan itu sendiri.
artinya 2/2 itu hasilnya 1 jadi 1/2 dikalikan dengan 1 ya hasilnya tetep setengah. oke ? mudah bukan.
mengubah bentuk pecahan biasa kedesimal dapat dilakukan dengan membagikan pembilang dengan penyebutnya. jika penyebutnya 10, 100, 1000, 10000, ... , maka banyaknya koma pada pecahan desimal sesuai dengan penyebutnya, artinya jika penyebutnya 10 maka hanya ada 1 angka dibelakang koma, jika 100 maka 2 angka dibelakang koma begitu seterusnya.
contoh :
1/10 = 0,1
1/100 = 0,01
1/1000 = 0,001
12/10000 = 0,0012
2/5 = ...
jadikan penyebutnya menjadi sepuluh dengan mengalikan 2 INGAT jika penyebutnya dikalikan dengan 2 maka begitu juga dengan pembilangnya.
2/5 x 2/2 = 4/10 maka bentuk desimal dari 2/5 adalah 0,4.
Mengubah pecahan desimal ke bentuk pecahan biasa
Dalam mengubah pecahan desimal ke pecahan biasa kita harus memperhatika berapa angka dibelakang koma dari pecahan desimal tersebut. INGAT !! jika ada 1 angka dibelakang koma berarti penyebutnya 10. seperti yang sudah dijelaskan diatas.
Untuk lebih mudahnya perhatika contoh berikut :
0,2 = 2/10 disederhanakan menjadi 1/5
0,25 = 25/100 disederhanakan menjadi 1/4
2,65 = 2 + 65/100 disederhanakan menjadi 2 13/20
mudah bukan. -_-
Mengubah pecahan biasa ke bentuk persen
untuk mengubah pecahan biasa menjadi persen yang wajib dilakukan adalah mengubah penyebut dari pecahan tersebut menjadi berpenyebut 100 atau mengalikan pecahan biasa tersebut dengan 100%
contoh :
1/4 = 1/4 x 25/25 ( kenapa dikalikan 25/25 ? ya benar untuk memperoleh penyebut 100 )
1/4 x 25/25 = 25/100 = 25%
oia tidak selalu pembilang dan penyebutnya dikalikan dengan bilangan 25 lho ya pengalian disesuaikan dengan penyebut dari pecahan biaa.
contoh lain 3/8
3/8 x 100% = 300/8 % = 37,5%
Admin cukupkan materi bilangan pecahan kali ini soalnya udah ngantuk dan mau makan sahur dulu ya udah laper berat nih soalnya :D.
pecahan a/b
a disebut dengan pembilang
b disebut dengan penyebut.
Jika pembilang dan penyebut suatu pecahan dikali ataupun dibagi dengan bilangan yang sama besar maka akan didapat pecahan yang senilai.
misal :
1/2 dikali dengan 2/2 maka hasilnya 2/4, nilai 1/2 = 2/4. meski bilangan pembilang dan penyebutnya berbeda akan tetapi nilainya tetap sama. Ingat invers dari perkalian ? ya benar berapapun bilangannya jika dikalikan dengan satu maka hasilnya adalah bilangan itu sendiri.
artinya 2/2 itu hasilnya 1 jadi 1/2 dikalikan dengan 1 ya hasilnya tetep setengah. oke ? mudah bukan.
Mengubah pecahan
Mengubah pecahan biasa kedalam bentuk pecahan desimal.mengubah bentuk pecahan biasa kedesimal dapat dilakukan dengan membagikan pembilang dengan penyebutnya. jika penyebutnya 10, 100, 1000, 10000, ... , maka banyaknya koma pada pecahan desimal sesuai dengan penyebutnya, artinya jika penyebutnya 10 maka hanya ada 1 angka dibelakang koma, jika 100 maka 2 angka dibelakang koma begitu seterusnya.
contoh :
1/10 = 0,1
1/100 = 0,01
1/1000 = 0,001
12/10000 = 0,0012
2/5 = ...
jadikan penyebutnya menjadi sepuluh dengan mengalikan 2 INGAT jika penyebutnya dikalikan dengan 2 maka begitu juga dengan pembilangnya.
2/5 x 2/2 = 4/10 maka bentuk desimal dari 2/5 adalah 0,4.
Mengubah pecahan desimal ke bentuk pecahan biasa
Dalam mengubah pecahan desimal ke pecahan biasa kita harus memperhatika berapa angka dibelakang koma dari pecahan desimal tersebut. INGAT !! jika ada 1 angka dibelakang koma berarti penyebutnya 10. seperti yang sudah dijelaskan diatas.
Untuk lebih mudahnya perhatika contoh berikut :
0,2 = 2/10 disederhanakan menjadi 1/5
0,25 = 25/100 disederhanakan menjadi 1/4
2,65 = 2 + 65/100 disederhanakan menjadi 2 13/20
mudah bukan. -_-
Mengubah pecahan biasa ke bentuk persen
untuk mengubah pecahan biasa menjadi persen yang wajib dilakukan adalah mengubah penyebut dari pecahan tersebut menjadi berpenyebut 100 atau mengalikan pecahan biasa tersebut dengan 100%
contoh :
1/4 = 1/4 x 25/25 ( kenapa dikalikan 25/25 ? ya benar untuk memperoleh penyebut 100 )
1/4 x 25/25 = 25/100 = 25%
oia tidak selalu pembilang dan penyebutnya dikalikan dengan bilangan 25 lho ya pengalian disesuaikan dengan penyebut dari pecahan biaa.
contoh lain 3/8
3/8 x 100% = 300/8 % = 37,5%
Admin cukupkan materi bilangan pecahan kali ini soalnya udah ngantuk dan mau makan sahur dulu ya udah laper berat nih soalnya :D.
Apa itu Kuadrat dan Akar Kuadrat ?
Kuadrat dan akar kuadrat
tampak asing ditelinga ketika dulu baru pertama kali mendengar kosakata
baru ini, ya akar kuadrat kali ini admin akan membahas pengertian akar
kuadrat disertai dengan contoh pembahasannya.
untuk sembarang bilangan bulat b maka :
b2 = b x b
kuadrat juga biasa disebut dengan pangkat 2.
Nilai √a = b jika b2 = a, dengan b merupakan bilangan positif atau nol.
Misal : √49 = 7, jawaban ini benar karena 72 = 49
Gimana sudah pahamkan cara menghitung akar kuadratnya ? pastinya sudah lah...
Demikian artikel sederhana mengenai kuadrat dan akar kuadrat yang bisa admin sajikan dan berikut tabel kuadrat dan akar kuadrat.
12 = 1
22 = 4
32 = 9
42 = 16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81
102 = 100
112 = 121
122 = 144
132 = 169
142 = 196
152 = 225
162 = 256
172 = 289
182 = 324
192 = 361
202 = 400
212 = 441
222 = 484
232 = 529
242 = 576
252 = 625
262 = 676
272 = 729
282 = 784
292 = 841
302 = 900
312 = 961
322 = 1024
332 = 1089
342 = 1156
352 = 1225
362 = 1296
372 = 1369
382 = 1444
392 = 1521
402 = 1600
412 = 1681
422 = 1764
432 = 1849
442 = 1936
452 = 2025
462 = 2116
472 = 2209
482 = 2304
492 = 2401
502 = 2500
512 = 2601
522 = 2704
532 = 2809
542 = 2916
552 = 3025
562 = 3136
572 = 3249
582 = 3364
592 = 3481
602 = 3600
612 = 3721
622 = 3844
632 = 3969
642 = 4096
652 = 4225
662 = 4356
672 = 4489
682 = 4624
692 = 4761
702 = 4900
712 = 5041
722 = 5184
732 = 5329
742 = 5476
752 = 5625
762 = 5776
772 = 5929
782 = 6084
792 = 6241
802 = 6400
812 = 6561
822 = 6724
832 = 6889
842 = 7056
852 = 7225
862 = 7396
872 = 7569
882 = 7744
892 = 7921
902 = 8100
912 = 8281
922 = 8464
932 = 8649
942 = 8836
952 = 9025
962 = 9216
972 = 9409
982 = 9604
992 = 9801
1002 = 10000
Untuk tabel akar kuadrat tinggal dibalik misal : √9801 = 99 . oke ? bisa dipahami kan ?
selamat belajar dan terus semangat. salam matika
Pengertian Kuadrat
Kuadrat suatu belangan adalah perkalian suatu bilangan dengan bilangan itu sendiri.untuk sembarang bilangan bulat b maka :
b2 = b x b
kuadrat juga biasa disebut dengan pangkat 2.
Pengertian Akar Kuadrat
√a adalah bilangan positif atau nol yang jika dikuadratkan menghasilkan a. Paham ? untuk lebih jelasnya silahkan perhatikan contoh berikut.Nilai √a = b jika b2 = a, dengan b merupakan bilangan positif atau nol.
Misal : √49 = 7, jawaban ini benar karena 72 = 49
Gimana sudah pahamkan cara menghitung akar kuadratnya ? pastinya sudah lah...
Demikian artikel sederhana mengenai kuadrat dan akar kuadrat yang bisa admin sajikan dan berikut tabel kuadrat dan akar kuadrat.
12 = 1
22 = 4
32 = 9
42 = 16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81
102 = 100
112 = 121
122 = 144
132 = 169
142 = 196
152 = 225
162 = 256
172 = 289
182 = 324
192 = 361
202 = 400
212 = 441
222 = 484
232 = 529
242 = 576
252 = 625
262 = 676
272 = 729
282 = 784
292 = 841
302 = 900
312 = 961
322 = 1024
332 = 1089
342 = 1156
352 = 1225
362 = 1296
372 = 1369
382 = 1444
392 = 1521
402 = 1600
412 = 1681
422 = 1764
432 = 1849
442 = 1936
452 = 2025
462 = 2116
472 = 2209
482 = 2304
492 = 2401
502 = 2500
512 = 2601
522 = 2704
532 = 2809
542 = 2916
552 = 3025
562 = 3136
572 = 3249
582 = 3364
592 = 3481
602 = 3600
612 = 3721
622 = 3844
632 = 3969
642 = 4096
652 = 4225
662 = 4356
672 = 4489
682 = 4624
692 = 4761
702 = 4900
712 = 5041
722 = 5184
732 = 5329
742 = 5476
752 = 5625
762 = 5776
772 = 5929
782 = 6084
792 = 6241
802 = 6400
812 = 6561
822 = 6724
832 = 6889
842 = 7056
852 = 7225
862 = 7396
872 = 7569
882 = 7744
892 = 7921
902 = 8100
912 = 8281
922 = 8464
932 = 8649
942 = 8836
952 = 9025
962 = 9216
972 = 9409
982 = 9604
992 = 9801
1002 = 10000
Untuk tabel akar kuadrat tinggal dibalik misal : √9801 = 99 . oke ? bisa dipahami kan ?
selamat belajar dan terus semangat. salam matika
Apa itu Bilangan Bulat ?
Materi Bilangan Bulat untuk tingkat SMP, kali ini admin akan share
mengenai apa itu bilangan bulat setelah beberapa minggu ini tidak pernah
posting akhirnya keluar lagi semangat untuk memberikan asupan materi
pada blog ini.
 Sebelum
membahas lebih lanjut mari kita kaji dulu pengertian bilangan bulat,
matematika tidak akan lepas dari yang namanya bilangan oleh karena itu
menguasai materi bilangan bulat juga termasuk penting kadang kita sering
lupa apa saja sih himpunan dari bilangan bulat itu sendiri.
Sebelum
membahas lebih lanjut mari kita kaji dulu pengertian bilangan bulat,
matematika tidak akan lepas dari yang namanya bilangan oleh karena itu
menguasai materi bilangan bulat juga termasuk penting kadang kita sering
lupa apa saja sih himpunan dari bilangan bulat itu sendiri.
Jadi secara ringkas bilangan bulat terdiri dari bilangan bulat negatif, bilangan bulat negatif dan nol. Lambang bilangan bulat disimbolkan dengan huruf Z (seperti gambar diatas ) yang berasal dari kata Zahlen (dari bahasa Jerman yang artinya "bilangan").
Dalam gambar garis bilangan diatas bilangan 2 terletak di sebelah kanan
bilangan -1 maka 2 lebih besar dari -1 bisa ditulis 2 > -1, -4
terletak disebelah kiri -2 maka -4 lebih kecil dari -1 ( -4 < -1 )
jadi dapat disimpulkan bahwa nilai bilangan semakin kekeri maka bilangan
itu semakin kecil dan sebaliknya jika semakin kekanan maka bilangan itu
semakin besar.
a. 7, ... -7
b. 10, ... ,-11
c. -45, ... , -20
d. -14, ... , 14
e. 56, ... ,-65
Penjumlahan dan sifatnya
Untuk mempermudah dalam memahami penjumlahan bilangan bulat kita dapat menggunakan bantuan garis bilangan, seperti contoh dibawah ini :
Tentukan hasil -4 + 3.
pertama tarik garis kekiri ( kenapa kekiri ? kan bilangannya negatif ) dari nol sampai -4 kemudian tarik garis kekanan sepanjang 3 skala, nah dapet deh jawabannya -1. mudah kan ?
Sifat komutatif penjumlahan
a + b = b + a, misal apa bila ada soal 6 + 3 itu sama dengan 3 + 6.
Sifat asosiatif penjumlahan
( a + b ) + c = a + ( b + c ), artinya kalian bisa menjumlahkan a dan b lebih dulu kemudian baru ditambah dengan c, atau b dan c dijumlahkan lebih dulu baru dijumlahkan dengan a.
Sampai disini dulu materi bilangan bulat nya dan materi ini dilanjutkan ke operasi bilangan bulat
 Sebelum
membahas lebih lanjut mari kita kaji dulu pengertian bilangan bulat,
matematika tidak akan lepas dari yang namanya bilangan oleh karena itu
menguasai materi bilangan bulat juga termasuk penting kadang kita sering
lupa apa saja sih himpunan dari bilangan bulat itu sendiri.
Sebelum
membahas lebih lanjut mari kita kaji dulu pengertian bilangan bulat,
matematika tidak akan lepas dari yang namanya bilangan oleh karena itu
menguasai materi bilangan bulat juga termasuk penting kadang kita sering
lupa apa saja sih himpunan dari bilangan bulat itu sendiri.Pengertian Bilangan Bulat
Bilangan bulat adalah sekumpulan bilangan yang anggotanya terdiri dari bilangan negatif dan bilangan cacah. dari pengertian tersebut dapat kita simpulkan bahwa bilangan bulat merupakan semua bilangan baik itu negatif atau positif termasuk juga nol. Tapi ingat pecahan tidak termasuk dalam bilangan bulat.Jadi secara ringkas bilangan bulat terdiri dari bilangan bulat negatif, bilangan bulat negatif dan nol. Lambang bilangan bulat disimbolkan dengan huruf Z (seperti gambar diatas ) yang berasal dari kata Zahlen (dari bahasa Jerman yang artinya "bilangan").
Bilangan bulat dalam garis bilangan
Didalam garis bilangan bilangan bulat dapat dinyatakan seperti pada gambar dibawah : |
| Bilangan negatif selalu digambarkan disebelah kiri |
Contoh soal bilangan bulat
Sisipkanlah lambang < atau > diantara pasangan bilangan berikut agar menjadi kalimat yang benar !a. 7, ... -7
b. 10, ... ,-11
c. -45, ... , -20
d. -14, ... , 14
e. 56, ... ,-65
Operasi Hitung Bilangan Bulat
Setelah memahami pengertian bilangan bulat diatas selanjutnya kita akan membahas mengenai bagaimana operasi bilangan bulat tambah, kurang, kali dan bagi serta sifat-sifat yang terkandung dalam operasi bilangan tersebut.Penjumlahan dan sifatnya
Untuk mempermudah dalam memahami penjumlahan bilangan bulat kita dapat menggunakan bantuan garis bilangan, seperti contoh dibawah ini :
Tentukan hasil -4 + 3.
pertama tarik garis kekiri ( kenapa kekiri ? kan bilangannya negatif ) dari nol sampai -4 kemudian tarik garis kekanan sepanjang 3 skala, nah dapet deh jawabannya -1. mudah kan ?
Sifat komutatif penjumlahan
a + b = b + a, misal apa bila ada soal 6 + 3 itu sama dengan 3 + 6.
Sifat asosiatif penjumlahan
( a + b ) + c = a + ( b + c ), artinya kalian bisa menjumlahkan a dan b lebih dulu kemudian baru ditambah dengan c, atau b dan c dijumlahkan lebih dulu baru dijumlahkan dengan a.
Sampai disini dulu materi bilangan bulat nya dan materi ini dilanjutkan ke operasi bilangan bulat
Operasi Hitung Bilangan Bulat
Lanjutan artikel apa itu bilangan bulat ,
artikel yang lalu masih sampai operasi hitung bilangan bulat mengenai
sifat komutatif dan asosiatif penjumlahan bilangan bulat.
Identitas penjumlahan.
untuk sembarang bilangan bulat berlaku a + 0 = a, artinya berapapun nilai bilangan bulat apabila dijumlahkan dengan 0 maka hasilnya bilangan itu sendiri.
Sifat Pengurangan Bilangan Bulat
Lawan ( invers penjumlahan ) dari a adalah -a . penjumlahan sembarang bilangan bulat dengan lawannya selalu menghasilkan nol. Jadi, untuk sembarang bilangan bulat berlaku a - b = (a + b)
contoh : 12 + (-12) = -12+12=0
Sifat tertutup pada perkalian
Untuk sembarang bilangan bulat a dan b, apabila dikalikan maka hasilnya pasti bilangan bulat.
contoh : 12 x 20 = 240
12 bilangan bulat
20 bilangan bulat
240 juga bilangan bulat
sifat komutatif perkalian
a x b = b x a
sifat asosiatif pembagian
( a x b ) x c = a x ( b x c )
Identitas perkalian
Jika sebelumnya sudah dijelaskan bahwa identitas penjumlahan adalah 0 (nol), sedang identitas perkalian adalah 1 ( satu )
a x 1 = 1 x a = a
berapapun bilangan apabila dikalikan dengan angka 1 ( satu ) maka hasilnya adalah bilangan itu sendiri.
perkalian dengan 0 (nol)
0 x a = a x 0 = 0
berapapun bilangannya apabila dikalikan dengan 0 maka hasilnya nol.
Sifat distributif
Pada sifat distributif perkalian dan penjumlahan berlaku :
a x (b + c ) = a x b + a x c
sifat distributif pengurangan
a x (b - c ) = a x b - a x c
Sifat pembagian bilangan bulat
hasil dari pembagian 2 bilangan bulat dapt ditentukan berdasarkan tanda bilangan dengan cara berikut :
(+) : (+) = (+) , bilangan postif dibagi dengan bilangan positif hasilnya positif
(+) : (-) = (-), bilangan postif dibagi dengan bilangan negatif hasilnya negatif
(-) : (+) = (-), bilangan negatif dibagi dengan bilangan positif hasilnya negatif
(-) : (-) = (+), bilangan negatif dibagi dengan bilangan negatif hasilnya positif
operasi hitung pembagian bilangan bulat tidak bersifat komutatif maupun asosiatif.
Selesai sudah penjelasan mengenai materi bilangan bulat, baik mengenai garis bilangan maupun operasi hitung bilangan bulat. semoga dapat di pahami dan dapat bermanfaat.
Selamat belajar
+Matematika academy
Identitas penjumlahan.
untuk sembarang bilangan bulat berlaku a + 0 = a, artinya berapapun nilai bilangan bulat apabila dijumlahkan dengan 0 maka hasilnya bilangan itu sendiri.
Sifat Pengurangan Bilangan Bulat
Lawan ( invers penjumlahan ) dari a adalah -a . penjumlahan sembarang bilangan bulat dengan lawannya selalu menghasilkan nol. Jadi, untuk sembarang bilangan bulat berlaku a - b = (a + b)
contoh : 12 + (-12) = -12+12=0
Sifat tertutup pada perkalian
Untuk sembarang bilangan bulat a dan b, apabila dikalikan maka hasilnya pasti bilangan bulat.
contoh : 12 x 20 = 240
12 bilangan bulat
20 bilangan bulat
240 juga bilangan bulat
sifat komutatif perkalian
a x b = b x a
sifat asosiatif pembagian
( a x b ) x c = a x ( b x c )
Identitas perkalian
Jika sebelumnya sudah dijelaskan bahwa identitas penjumlahan adalah 0 (nol), sedang identitas perkalian adalah 1 ( satu )
a x 1 = 1 x a = a
berapapun bilangan apabila dikalikan dengan angka 1 ( satu ) maka hasilnya adalah bilangan itu sendiri.
perkalian dengan 0 (nol)
0 x a = a x 0 = 0
berapapun bilangannya apabila dikalikan dengan 0 maka hasilnya nol.
Sifat distributif
Pada sifat distributif perkalian dan penjumlahan berlaku :
a x (b + c ) = a x b + a x c
sifat distributif pengurangan
a x (b - c ) = a x b - a x c
Sifat pembagian bilangan bulat
hasil dari pembagian 2 bilangan bulat dapt ditentukan berdasarkan tanda bilangan dengan cara berikut :
(+) : (+) = (+) , bilangan postif dibagi dengan bilangan positif hasilnya positif
(+) : (-) = (-), bilangan postif dibagi dengan bilangan negatif hasilnya negatif
(-) : (+) = (-), bilangan negatif dibagi dengan bilangan positif hasilnya negatif
(-) : (-) = (+), bilangan negatif dibagi dengan bilangan negatif hasilnya positif
operasi hitung pembagian bilangan bulat tidak bersifat komutatif maupun asosiatif.
Selesai sudah penjelasan mengenai materi bilangan bulat, baik mengenai garis bilangan maupun operasi hitung bilangan bulat. semoga dapat di pahami dan dapat bermanfaat.
Selamat belajar
+Matematika academy
Tabel Angka Romawi Terlengkap (1-1000)
Ada yang tanya menulis angka romawi 11 itu gimana sih...? saya jawab aja
XI, itulah yang jadi alasan kenapa saya posting tabel angka romawi,
ternyata seperti kelihatannya mudah tapi banyak anak-anak yang kurang
paham untuk menuliskan angka romawi.
Kadang untuk menuliskan angka romawi 8, angka romawi 10, angka romawi 12
atau lain sebagainya anak-anak masih mengalami kesulitan, berikut admin
bagikan tabel angka romawi lengkap dari 1 sampai 1000. Jika anda
seorang guru silahkan anak didik kalian berikan printout tabel angka
romawi berikut agar dapat digunakan sebagai pembelajaran.
 |
| tabel angka romawi |
Silahkan download gambar diatas untuk dapat melihat dengan lebih jelas.
Untuk memudahkan menghafal tabel romawi matematika tersebut kita ambil point penting2nya saja :
Misal
10 = X
20 = XX
30 = XXX
40 = XL
50 = L
60 = LX
70 = LXX
80 = LXXX
90 = XC
100 = C
500 = D
1000 = M
Biasanya penulisan angka romawi yang sering mengalami kesalahan yaitu
pada angka 40 dan 90 karena kadang anak-anak sering menuliskan romawi 40
dengan XXXX begitu juga kesalahan dalam penulisan romawi 90 dengan
LXXXX ini kesalahan yang sering dilakukan anak-anak.
Ketika kita sudah bisa menghafalkan point-point penting angka romawi
diatas tentunya bukan halsulit untuk dapat mentranslate angka-angka
dalam bentuk angka romawi :)
misal kita ankan rubah angka 1574
untuk lebih mudahnya kita pecah menjadi 1000+500+70+4 = M+D+LXX+IV
Maka kita akan mendapatkan bahwa angka romawi dari 1574 adalah MDLXXIV
Contoh lainnya penulisan angka romawi kuno :
1. 16 = XVI
2. 35 = XXXV
3. 45 = XLV
4. 79 = LXXIX
5. 99 = IC
6. 110 = CX
7. 999 = CMXCIX
8. 1666 = MDCLXVI
9. 2014 = MMXIV
Beberapa kekurangan atau kelemahan sistem angka romawi, yakni :
1. Tidak ada angka nol / 0
2. Terlalu panjang untuk menyebut bilangan tertentu
3. Terbatas untuk bilangan-bilangan kecil saja
Download Tabel Perkalian Terlengkap
Tabel perkalian, apa sih fungsinya ?
kalo kita sudah menghafal banyak perkalian mungkin kita tidak membutuhkan lagi tabel perkalian untuk membantu kita dalam berlajar perkalian matematika. Masih ingat waktu SD dulu saya memiliki buku yang bagian sampul belakangnya ada tabel perkalian matematikanya. Kalian punya?
Tapi ya namanya juga dulu tabelnya ya seperti itu0itu saja nggak ada perkembangan padahal tabel perkalian matematika tidak hanya seperti itu saja jadi tampak menjenuhkan, tanpa warna warni :) tapi senangnya tabel itu membantu pada saat mengikuti ujian he he he
kali ini belajar-soal-matematika.blogspot.com akan memberikan tabel perkalian matematika yang dapat membantu kalian belajar juga, selain tabel perkalian secara tidak langsung tabel perkalian ini juga dapat digunakan sebagai tabel kuadrat. kok bisa silahkan lihat saja gambar berikut.
kalo kita sudah menghafal banyak perkalian mungkin kita tidak membutuhkan lagi tabel perkalian untuk membantu kita dalam berlajar perkalian matematika. Masih ingat waktu SD dulu saya memiliki buku yang bagian sampul belakangnya ada tabel perkalian matematikanya. Kalian punya?
Tapi ya namanya juga dulu tabelnya ya seperti itu0itu saja nggak ada perkembangan padahal tabel perkalian matematika tidak hanya seperti itu saja jadi tampak menjenuhkan, tanpa warna warni :) tapi senangnya tabel itu membantu pada saat mengikuti ujian he he he
kali ini belajar-soal-matematika.blogspot.com akan memberikan tabel perkalian matematika yang dapat membantu kalian belajar juga, selain tabel perkalian secara tidak langsung tabel perkalian ini juga dapat digunakan sebagai tabel kuadrat. kok bisa silahkan lihat saja gambar berikut.
silahkan lihat bagian gambar tabel perkalian tersebut yang berwarna
merah diagoal dengan bilangan 0, 1, 4, 9, ....144 nah itulah yang admin
sebut sebagai tabel kuadratik, ada yang menemukan pola dalam tabel
perkalian tersebut?
Ya benar nilai angka-angka yang ada di atas diagonal dan di bawah diagonal kuadrat menunjukkan angka-angka dengan nilai sama.
silahkan kalian pelajari tabel perkalian matematika tersebut kalo mau ya silahkan dbuat sampai angka 100 menggunakan microsoft exel. saya yakin kalian bisa.
untuk mendownload tabel perkalian tersebut silahkan save as aja gambarnya. terimakasih sudah berkunjung dan sampai jumpa lain waktu.
Cara Belajar Operasi Hitung Campuran
Operasi hitung campuran,
kadang siswa sulit untuk menentukan bagaimana sih cara belajar perasi
hitung campuran? manasih yang harus dikerjakan terlebih dahulu. Itu yang
menjadi tantangan seorang guru untuk memberikan kepahaman kepada anak
didiknya.
Untuk memberikan cara belajar operasi hitung kali ini, belajar-soal-matematika.blogspot.com akan memberikan contoh mengenai cara menentukan selisih usia Ayah dan Ibu, untuk mengerjakan operasi hitung campuran kita akan menggunakan Rumus matematika KABATAKU ( kali, bagi, tambah, kurang )
Untuk memberikan cara belajar operasi hitung kali ini, belajar-soal-matematika.blogspot.com akan memberikan contoh mengenai cara menentukan selisih usia Ayah dan Ibu, untuk mengerjakan operasi hitung campuran kita akan menggunakan Rumus matematika KABATAKU ( kali, bagi, tambah, kurang )
operasi hitung campuran pada pecahan berlaku beberapa aturan antara lain :
- Perkalian dan pembagian dikerjakan terlebih dahulu daripada penjumlahan dan pengurangan.
- Jika dalam soal terdapat tanda kurung, kerjakan terlebih dahulu yang diberi tanda kurung
Untuk memperdalam materi operasi hitung campuran
pada pecahan mengenai bentuk perkalian dikerjakan terlebih dahulu dan
ubahlah bentuk pecahan campuran menjadi pecahan biasa dapat anda lihat
pada contoh soal seperti dibawah ini
Soal:
Diketahui:
- Jumlah Umur Ayah dan Umur Ibu adalah 90 tahun
- Umur ayah : umur ibu = 8 :7
ditanyakan berapakah umur ayah?
jawab :
Nah sekian dulu artikel mengenai Operasi
Hitung Campuran, semoga kalian bisa memahami dan memberikan kepahaman
pada teman saudara tetangga atau yang lainnya he he :D, terima kasih
sudah berkunjung di blog sederhana ini, silahkan di share jika menurut
anda artikel matematika ini bermanfaat.
Soal:
Diketahui:
- Jumlah Umur Ayah dan Umur Ibu adalah 90 tahun
- Umur ayah : umur ibu = 8 :7
ditanyakan berapakah umur ayah?
Download Rangkuman Materi UN Matematika SMA IPA
Ujian Nasional tahun 2014 sebentar lagi makanya admin coba memberikan beberapa rangkuman materi un matematika sma IPA pada postingan kali ini dengan harapan dapat membatu kalian yang akan mengikuti ujian nasional tahun 2014.
Mari sambut ujian nasional dengan lapang tanpa ketakutan sama sekali, kok bisa...? karena dengan persiapan yang matang jauh-jauh hari dapat meningkatkan kepercayaan diri lebih untuk menghadapi tantangan ujian nasional.
Soal-soal ujian nasioanal yang sudah di standari sasi sebenarnya tidak terlalu berat karena sudah disesuaikan dengan kemampuan anak didik di indonesia. konsep yang matang merupakan salah satu hal yang dapat mendukung untuk dapat mengikuti ujian nasional dengan baik.
Makanya blog belajar-soal-matematika.blogspot.com akan memberikan rangkuman materi UN matematika SMA IPA tahun 2013 dengan harapan dapat membantu anda untuk menyiapkan diri. Lho kok yang tahun 2013? Kalo untuk yang sesuai dengan indikator-indikator pada kisi-kisi SKL Ujian Nasional tahun 2014 diartikel kelanjutannya, makanya pantengin terus yah blog sederhana ini.
Berikut ini rangkuman & ringkasan materi penting pelajaran Matematika SMA IPA yang keluar dalam Ujian Nasional tahun 2013 :
- Iingkaran atau kesetaraan pernyataan majemuk atau pernyataan berkuantor
- Diskriminan persamaan atau fungsi kuadrat
- Persamaan lingkaran atau garis singgung lingkaran
- Fungsi komposisi atau fungsi invers
- Matriks
- Sudut antara dua vektor
- Transformasi geometri
- Fungsi eksponen atau fungsi logaritma
- Jarak dan sudut dua objek di ruang
- Persamaan trigonometri
- Limit fungsi aljabar atau limit fungsi trigonometri
- Integral tak tentu dan tertentu dari fungsi aljabar dan fungsi trigonometri
- Statistik: ukuran pemusatan
- Peluang
- Penarikan Kesimpulan beberapa premis
- Aturan pangkat, akar, dan logaritma
- Rumus jumlah dan hasil kali akar-akar persamaan kuadrat
- Sistem persamaan linear
- Teorema sisa dan teorema faktor suku banyak
- Program linear
- Operasi aljabar vektor
- Proyeksi vektor
- Pertidaksamaan eksponen atau logaritma
- Deret aritmetika dan geometri
- Aturan sinus dan aturan kosinus
- Jumlah dua nilai trigonometri atau jumlah dua sudut trigonometri
- Aplikasi fungsi turunan
- Aplikasi integral luas daerah dan volum benda putar
- Aturan pencacahan, permutasi dan kombinasi
Silahkan Download Rangkuman Materi UN Matematika SMA IPA disini
Sekian aja artikel kali ini semoga dapat bermanfaat untuk kita semua dan selamat menghadapi ujian nasional 2014 nanti dan semoga mendapatkan hasil yang memuaskan Amiin.
teri kasih sudah berkunjung untuk rangkuman materi ujian nasional matematika SMA IPA tahun 2014nya tunggu aja di blog sederhana ini kalo nggak ya like aja fanpage "matematika" untuk dapat mengetahui sewaktu-waktu kalo admin update lagi.
Mari sambut ujian nasional dengan lapang tanpa ketakutan sama sekali, kok bisa...? karena dengan persiapan yang matang jauh-jauh hari dapat meningkatkan kepercayaan diri lebih untuk menghadapi tantangan ujian nasional.
Soal-soal ujian nasioanal yang sudah di standari sasi sebenarnya tidak terlalu berat karena sudah disesuaikan dengan kemampuan anak didik di indonesia. konsep yang matang merupakan salah satu hal yang dapat mendukung untuk dapat mengikuti ujian nasional dengan baik.
Makanya blog belajar-soal-matematika.blogspot.com akan memberikan rangkuman materi UN matematika SMA IPA tahun 2013 dengan harapan dapat membantu anda untuk menyiapkan diri. Lho kok yang tahun 2013? Kalo untuk yang sesuai dengan indikator-indikator pada kisi-kisi SKL Ujian Nasional tahun 2014 diartikel kelanjutannya, makanya pantengin terus yah blog sederhana ini.
Berikut ini rangkuman & ringkasan materi penting pelajaran Matematika SMA IPA yang keluar dalam Ujian Nasional tahun 2013 :
- Iingkaran atau kesetaraan pernyataan majemuk atau pernyataan berkuantor
- Diskriminan persamaan atau fungsi kuadrat
- Persamaan lingkaran atau garis singgung lingkaran
- Fungsi komposisi atau fungsi invers
- Matriks
- Sudut antara dua vektor
- Transformasi geometri
- Fungsi eksponen atau fungsi logaritma
- Jarak dan sudut dua objek di ruang
- Persamaan trigonometri
- Limit fungsi aljabar atau limit fungsi trigonometri
- Integral tak tentu dan tertentu dari fungsi aljabar dan fungsi trigonometri
- Statistik: ukuran pemusatan
- Peluang
- Penarikan Kesimpulan beberapa premis
- Aturan pangkat, akar, dan logaritma
- Rumus jumlah dan hasil kali akar-akar persamaan kuadrat
- Sistem persamaan linear
- Teorema sisa dan teorema faktor suku banyak
- Program linear
- Operasi aljabar vektor
- Proyeksi vektor
- Pertidaksamaan eksponen atau logaritma
- Deret aritmetika dan geometri
- Aturan sinus dan aturan kosinus
- Jumlah dua nilai trigonometri atau jumlah dua sudut trigonometri
- Aplikasi fungsi turunan
- Aplikasi integral luas daerah dan volum benda putar
- Aturan pencacahan, permutasi dan kombinasi
Silahkan Download Rangkuman Materi UN Matematika SMA IPA disini
Sekian aja artikel kali ini semoga dapat bermanfaat untuk kita semua dan selamat menghadapi ujian nasional 2014 nanti dan semoga mendapatkan hasil yang memuaskan Amiin.
teri kasih sudah berkunjung untuk rangkuman materi ujian nasional matematika SMA IPA tahun 2014nya tunggu aja di blog sederhana ini kalo nggak ya like aja fanpage "matematika" untuk dapat mengetahui sewaktu-waktu kalo admin update lagi.
Pecahan - materi pendalaman un matematika sd kelas 6
Dalam ebook yang akan saya bagikan ini sudah disediakan penjelasan lengkap mengenai pecahan yang bisa digunakan untuk referensi menghadapi ujian nasional (un) khususnya mata pelajaran matematika tingkat sekolah dasar.
Daftar materi matematika pecahan dalam ebook ini :
Mengubah Menjadi Pecahan yang Senilai
Menyederhanakan Pecahan
Mengurutkan Pecahan
Mengubah Bentuk Pecahan Menjadi Bentuk Desimal
Mengubah Pecahan Biasa Menjadi Bentuk Desimal
Mengubah Pecahan Campuran Menjadi Bentuk Desimal
Mengubah Bentuk Persen Menjadi Bentuk Desimal
Mengubah Bentuk Pecahan Persen Menjadi Bentuk Persen
Nilai Pecahan Suatu Bilangan
Menentukan Nilai Pecahan dari Suatu Bilangan
Nilai Pecahan atau Persentase dari Besaran Tertentu
Operasi Hitung pada Pecahan
Penjumlahan dan Pengurangan pada Pecahan
Penjumlahan dan pengurangan Pecahan Desimal
Perkalian dan Pembagian pada Pecahan Biasa dan Campuran
Perkalian dan Pembagian Pecahan Desimal
Operasi Hitung Campuran pada Pecahan
Perbandingan
Pecahan sebagai Perbandingan
Menyelesaikan Soal Cerita
Perbandingan Senilai
Skala
Itulah materi sub-bab yang didalam materi ini, jika kalian ingin mendapatkan materi ini silahkan menuju kemari pecahan,
Semoga materi pecahan ini dapat bermanfaat untuk kita semua, terima kasih sudah mau berkunjung di blog sederhana ini. lihat juga materi matematika lainnya disini
Daftar materi matematika pecahan dalam ebook ini :
Mengubah Menjadi Pecahan yang Senilai
Menyederhanakan Pecahan
Mengurutkan Pecahan
Mengubah Bentuk Pecahan Menjadi Bentuk Desimal
Mengubah Pecahan Biasa Menjadi Bentuk Desimal
Mengubah Pecahan Campuran Menjadi Bentuk Desimal
Mengubah Bentuk Persen Menjadi Bentuk Desimal
Mengubah Bentuk Pecahan Persen Menjadi Bentuk Persen
Nilai Pecahan Suatu Bilangan
Menentukan Nilai Pecahan dari Suatu Bilangan
Nilai Pecahan atau Persentase dari Besaran Tertentu
Operasi Hitung pada Pecahan
Penjumlahan dan Pengurangan pada Pecahan
Penjumlahan dan pengurangan Pecahan Desimal
Perkalian dan Pembagian pada Pecahan Biasa dan Campuran
Perkalian dan Pembagian Pecahan Desimal
Operasi Hitung Campuran pada Pecahan
Perbandingan
Pecahan sebagai Perbandingan
Menyelesaikan Soal Cerita
Perbandingan Senilai
Skala
Itulah materi sub-bab yang didalam materi ini, jika kalian ingin mendapatkan materi ini silahkan menuju kemari pecahan,
Semoga materi pecahan ini dapat bermanfaat untuk kita semua, terima kasih sudah mau berkunjung di blog sederhana ini. lihat juga materi matematika lainnya disini
Fungsi, Persamaan, dan Pertidaksamaan Eksponen dan Logaritma
Posting kali ini yang singkat singkat saja yaitu mengenai ringkasan
materi matematika untuk SMA kelas 12 BAB Fungsi, Persamaan, dan
Pertidaksamaan Eksponen dan Logaritma.
Berikut ringkasannya:
Berikut ringkasannya:
gimana ringkasan materi dan disertai rumus Fungsi, Persamaan, dan Pertidaksamaan Eksponen dan Logaritma, kurang lengkap? ^_^ udah pahami tuh rumus-rumusnya moga aja kalian bisa ya
Materi matematika vektor kelas 12 prog. IPA
Pengertian vektor menurut wikipedia
Vektor dalam matematika dan fisika adalah obyek geometri yang memiliki besar dan arah. Vektor jika digambar dilambangkan dengan tanda panah (→) . Besar vektor proporsional dengan panjang panah dan arahnya bertepatan dengan arah panah. Vektor dapat melambangkan perpindahan dari titik A ke B. Vektor sering ditandai sebagai

kali ini belajar-soal-matematika.blogspot.com akan memberikan materi matematika tentang Vektor untuk kalian yang masih duduk dibangku SMA kelas 12 jurusan program studi IPA.
didalam materi yang sudah saya upload dalam bentuk pdf ini menerangkan tentang vektor, bagaimana cara memahami tentang vektor sehingga kita lebih mengerti pengertian vektor itu sendiri.
dalam ebook matematika ini juga dilengkapi tentang contoh-contoh yang berhubungan dengan materi vektor dengan disertai pembahasannya lengkap.
Bab dan sub bab dalam materi vektor kelas 12 prog. IPA
A. Pengertian Vektor
B. Operasi pada vektor
dalam sub bab ini dijelaskan mengenai :
1. Penjumlahan dan Pengurangan Vektor
ada 2 cara dalam penjumlahan vektor yaitu dengan cara segitiga dan cara jajar genjang
2. Perkalian Skalar dengan vektor
3. sifat-sifat operasi hitung pada vektor
C. Perbandingan vektor
D. Perbandingan skalar dua vektor dan proyeksi vektor



























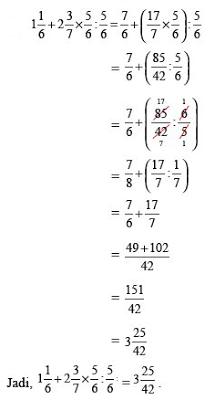




0 komentar:
Posting Komentar